Sorting data is a very common task and there are variety of algorithms to do the same (QuickSort, BubbleSort, MergeSort Etc … ). Not all of them are however suited for CUDA Architecture. Its important to bear that in mind, as people occasionally forces you to do something without the underlying information whether that is even possible – keep your own head, stay informed and make proper decisions based on your knowledge. A very simple example is to try to parallelize the Fibonacci sequence, which simply cannot be ported to CUDA as data needs to processed in parallel, yet for this sequence, you have to know values of samples [N-1] and [N-2] in order to compute a new value [N].
Bitonic sort works the way that it creates a so called “Bitonic sequences“,which grow in size as the algorithm’s progresses. The smallest Bitonic sequence is a sequence of 2 random values. The bitonic sequence rises up to its maximum value and then falls down to its minimum value. Another example of a 4-sample sequence: [1,8,6,3]. The bitonic sort algorithm therefore works such that it creates sequences of 2, then 4,8 and so on. In order to create such a sequence, each step has its own substage as shown below for the 16-sample sequence (3 Stages):
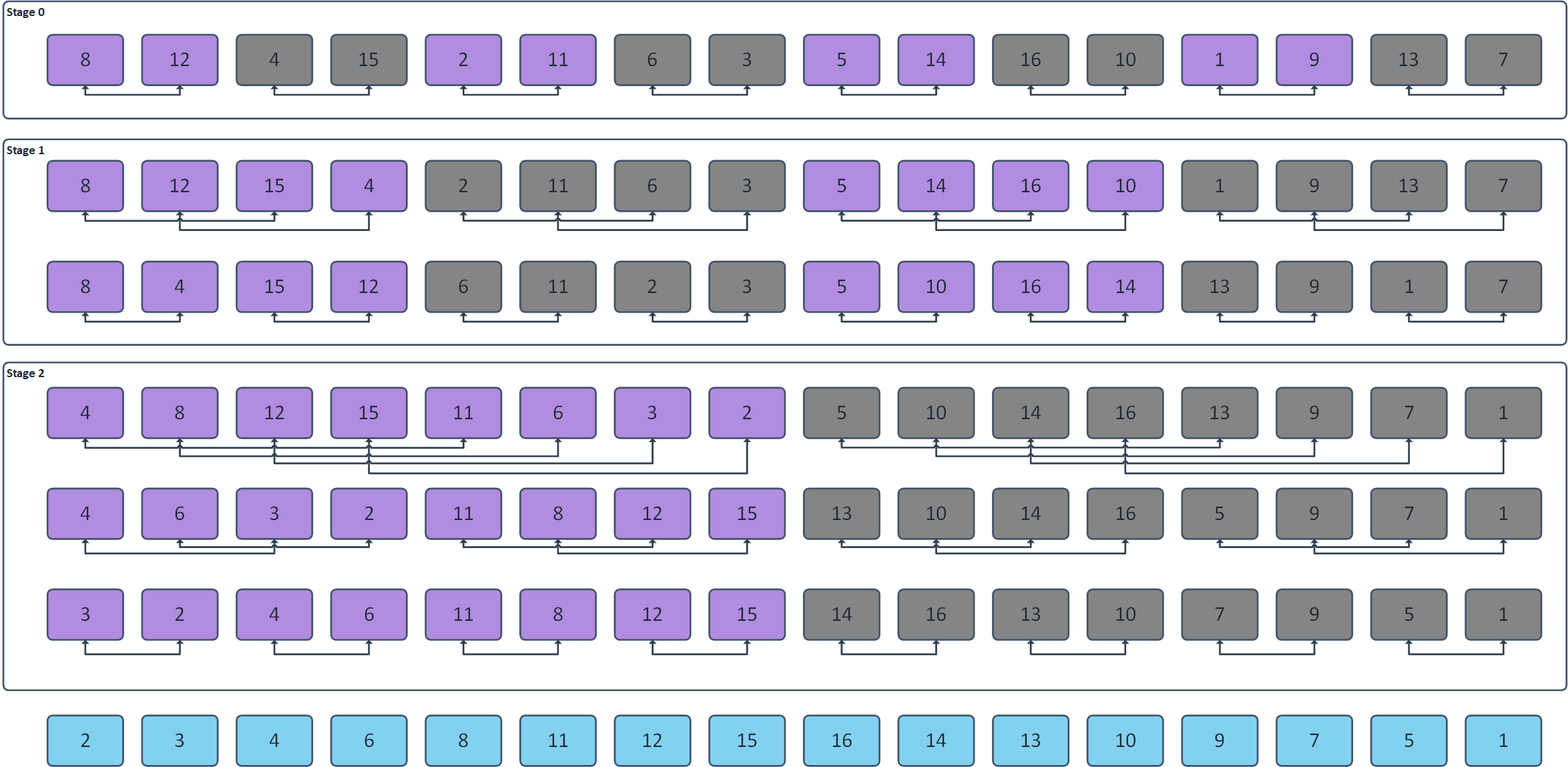
The algorithm works the way,that it compares two values and optionally swaps them in memory. Each connector therefore represent a comparator whether to swap or not. I have specifically used Violet Color to show sequences, which must be rising (IE: Left value smaller than right value) and Dark Gray color to show sequences, which must be falling (IE: Left value larger than right value). Note that in order to sort N samples, only N/2 threads is required. The algorithm can be efficiently put into the shared memory – So that bitonic sequences of up to approximately 1024 elements can be created. The rest must be processed in the global memory. As by the definition of swapping data within memory, this algorithm will be likely limited by memory throughput (And that’s why usage of shared memory is appreciated – I have however omitted that kernel. More curious researches are free to give it a try and port it to shared memory ?)
/**************************************
* @brief: Simple Bitonic Kernel Sorter
*************************************/
__global__ void Bitonic_Kernel(int*Global,unsigned int N,unsigned int Stage,unsigned int Dist){
unsigned int tix = threadIdx.x + blockIdx.x * blockDim.x;
if (tix < (N / 2)) {
unsigned int StagePw_C = (1 << (Stage + 0)); // 2^ (Stage + 0)
unsigned int StagePw_N = (1 << (Stage + 1)); // 2^ (Stage + 1)
unsigned int ThreadBaseInd = (tix % Dist) + ((tix / Dist) << 1) * Dist; // mod(tid,Dist) + (intdev(tid,Dist) * 2 * Dist)
// ------------------
// -- Data Indexes --
unsigned int Left_Ind = ThreadBaseInd;
unsigned int Right_Ind = ThreadBaseInd + Dist;
// --------------------------------------
// ------ Load From Global Memory -------
int Left = Global[Left_Ind];
int Right = Global[Right_Ind];
// -------------------------------------------------------------
// ------- Compute Sequence Direction (Rising / Falling) -------
unsigned int Sequence_Dir = (tix % StagePw_N);
if (Sequence_Dir < StagePw_C){
// ------------------------------
// ------- Rising Sequence ------
if (Right < Left) {
Global[Right_Ind] = Left;
Global[Left_Ind] = Right;
}
}else {
// --------------------------------
// ------- Falling Sequence -------
if (Right > Left) {
Global[Right_Ind] = Left;
Global[Left_Ind] = Right;
}
}
}
}As always, I do highly recommend to verify you implementation. That’s why also a CPU variant of the algorithm is appreciated. If you are however lazy as I am, then you will be likely satisfied with a simple check, that the final sequence is rising and then falling – this is also a sufficient check. The Stage / substage looping is done on the host CPU – Launching multiple kernels is usually okay (Given that the Kernel has enough work to do) – but here, its just occasionally swapping values within memory and what more, its important to note, that for example in order to sort a sequence, a total amount of kernel calls sum(1 : log2(N) – 1) is required! IE. 45 Calls for N = 1024 and 190 Calls for N = 1024*1024. That is also one of the reasons why including shared memory kernels will help a lot with performance. By the way – always think twice if you need to use some floating point arithmetic for indexing – using fmod / exp functions will slow everything down, whenever possible, take advantage of << or >> operators ?
Feel free again to see the underlying host code routines ➡️ HERE ⬅️ 😇