Differential Equations
And thus it was, that one day, I have decided to create a simulation of Satellite’s movement around the Earth by numerically solving differential equations. To be honest, I wanted to know how the satellite’s movements can be estimated. But numerically solving the related equations is actually not the way of how that is done in modern GNSS systems mostly due to the fact of error accumulation over time. Simply said, each numerical method has some kind of error and the more iterations we make, the less accurate the results are over time. As such, it cannot be used to perform any long-term GNSS calculations. Still, its quite suitable for a nice demo of Newton’s Second Law and Gravity in general. The most important parts of the simulation is the relation between the gravitational force and the centrifugal force as shown below.

One can easily estimate the required orbital speeds to reach circular orbit. For example, GPS satellites are located at the MEO (Medium Earth Orbit) with an altitude of 22 000km and a speed of 3.8km/s – Very close to circular trajectory. Based on the equations above, one of the sitations below might occur with the object’s trajectory:
- The object has exactly a circular orbit ( V = V1)
- The object will eventually crash into the Earth’s surface ( V < V1)
- The object will move with elliptical trajectory (V > V1 & V < V2)
- The object will just fly away → → → ( V > V2)

One can also define the third orbital speed as the escape speec fromt he Sun’s gravitational pull,but this is not of our interest of this demo, as it includes an Earth and a Satellite only. The simulation can be however extended quite easily to support 3D movement as well as to take into account forces of other objects (Planets and or Sun for example). For cartesian coordinate system (Such as this demo), the overall force onto an object needs to be divided into X and Y components. “–” just stands for the direction of the force. Furthermore, its quite obvious that acceleration is a second derivative of position and as such, we can rewrite the equations above to:

The problem here is, that most numerical methods deal with first order ordinary differential equations (ODEs). As such, we need to rewrite the system into a set of 4 first-order differential equations. Since we know that first derivative of position is the speed, we can substitue for speed (dx/dt = v). At this point, it is also quite obvious that in order to solve the set numerically, we need to supplement the initial conditions for each of those 4 equations:
- [X & Y ] Position
- [X & Y] Velocity

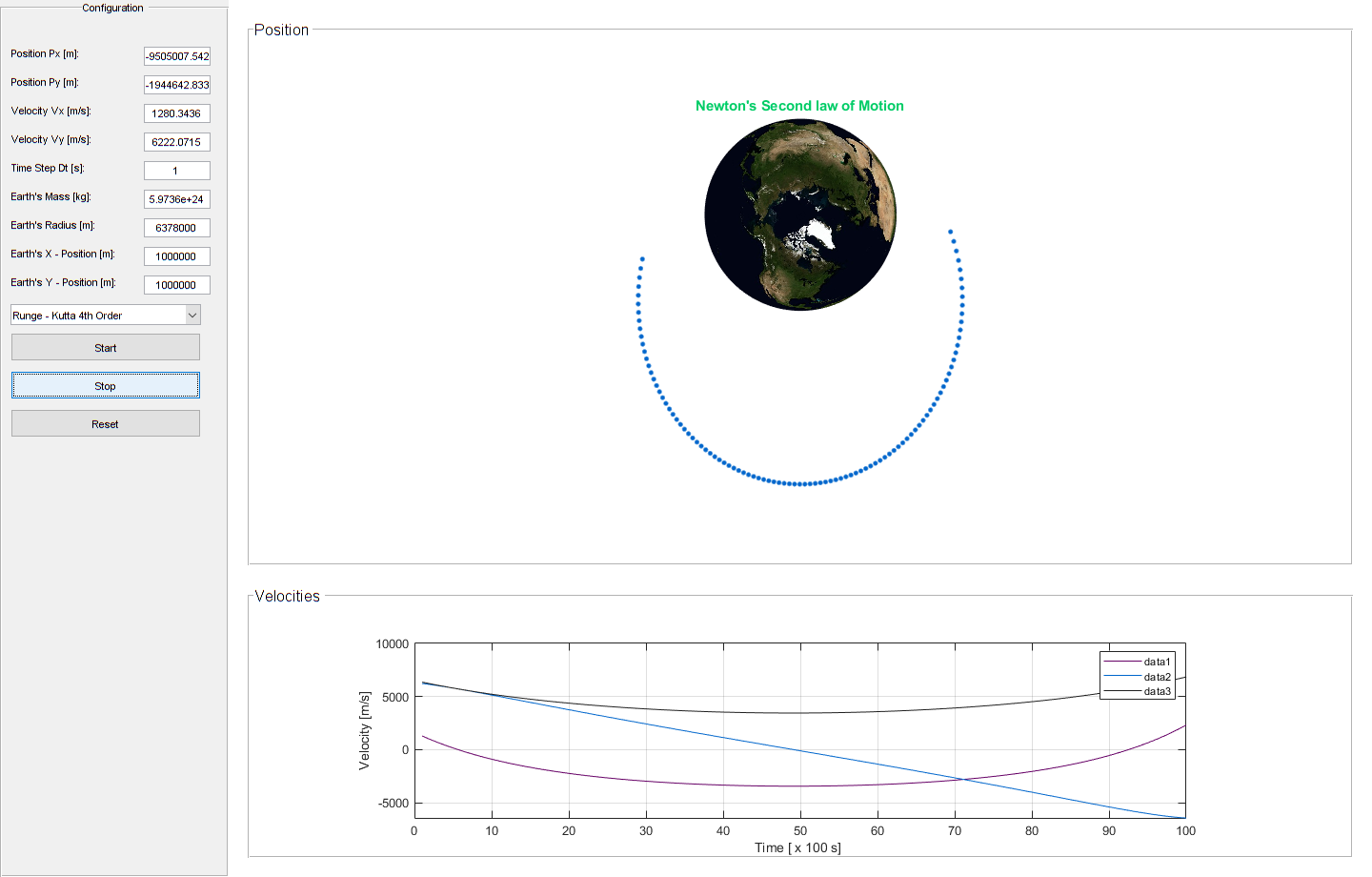
The simulation basically consists of a few buttons and a timer. There are 3 methods available for solving the equation. The most simple, Euler’s method, Second Order Runge-Kutta and the most commonly used Runge-Kutta 4th order. The methods do have a fixed step size, which is adjustable and defaults to single second. I havent implemnted the predictor-corrector methods so far. The biggest challenge for me was to adjust the standard solvers for second order ODE. One may also try to adjust the scripts to use the matlab’s build-in ODE solvers,which I have not tried yet.
As always, the entire project is available ➡️ HERE ⬅️. It doesn’t include any CUDA acceleration libraries as this task is not appropriate for GPU architecture.